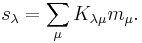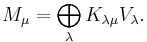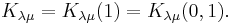Kostka number

In mathematics, a Kostka number K_λμ, introduced by Kostka (1882), is a non-negative integer depending on two partitions λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ. They can be used to express Schur polynomials s_λ as a linear combination of monomial symmetric functions m_μ:

$s_\lambda= \sum_\mu K_{\lambda\mu}m_\mu.\$

Kostka numbers also express the decomposition of the permutation module M_μ in terms of the representations V_λ corresponding to the character s_λ, i.e.

$M_\mu = \bigoplus_{\lambda} K_{\lambda \mu} V_\lambda.$

On the level of representations of 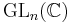$\mathrm{GL}_n(\mathbb{C})$ , the Kostka number K_λμ counts the dimension of the weight space corresponding to μ in the irreducible representation V_λ (where we require μ and λ to have at most n parts).

Kostka numbers are special values of the 1 or 2 variable Kostka polynomials:

$K_{\lambda\mu}= K_{\lambda\mu}(1)=K_{\lambda\mu}(0,1).$

Examples

The Kostka numbers for partitions of size at most 3 are given by the coefficients of:

s = m = 1 (indexed by the empty partition)

s₁ = m₁

s₂ = m₂ + m₁₁

s₁₁ = m₁₁

s₃ = m₃ + m₂₁ + m₁₁₁

s₂₁ = m₂₁ + 2m₁₁₁

s₁₁₁ = m_111.

Kostka (1882, pages 118-120) gave tables of these numbers for partitions of numbers up to 8.

References

Kostka, C. (1882), "Über den Zusammenhang zwischen einigen Formen von symmetrischen Funktionen", Crelle's J. 93: 89–123, http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=259790
Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144, http://www.oup.com/uk/catalogue/?ci=9780198504504
Sagan, Bruce E. (2001), "Schur functions in algebraic combinatorics", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=s/s120040